Biểu diễn miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}y – 2x \le 2\\y \le 4\\x \le 5\\x + y \ge – 1\end{array} \right.\) trên mặt phẳng tọa độ.
Từ đó tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F\left( {x;y} \right) = – x – y\) với \(\left( {x;y} \right)\) thỏa mãn hệ trên.
Phương pháp giải – Xem chi tiết
– Biểu diễn các miền nghiệm của từng bất phương trình \(y – 2x \le 2\); \(y \le 4\); \(x \le 5\) và \(x + y \ge – 1\) trên cùng một mặt phẳng tọa độ.
Bước 1: Vẽ đường thẳng \(ax + by = c\)
Bước 2: Lấy điểm một điểm không thuộc đường thẳng \(ax + by = c\) và thay vào bất phương trình cần xác định miền nghiệm.
Bước 3: Nếu tọa độ điểm đó thỏa mãn bất phương trình thì miền nghiệm của bất phương trình chứa điểm đó.
– Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F\left( {x;y} \right) = – x – y\)
Bước 1: Xác định các đỉnh của đa giác
Bước 2: Tính giá trị \(F\left( {x;y} \right) = – x – y\) tại các đỉnh đó và kết luận.
Lời giải chi tiết
Bước 1: Vẽ đường thẳng \(d_1: y-2x=2\) đi qua (0;2) và (-1;0).
Lấy điểm O(0;0) không thuộc \(d_1\). Vì 0-2.0=0<2 nên O thuộc miền nghiệm
Miền nghiệm của BPT \(y – 2x \le 2\) là nửa mp bờ \(d_1\), chứa điểm O.
Bước 2: Vẽ đường thẳng \(d_2: y=4\) đi qua (0;4) và (1;4)
Lấy điểm O(0;0) không thuộc \(d_2\). Vì 0<4 nên O thuộc miền nghiệm.
Miền nghiệm của BPT \(y \le 4\) là nửa mp bờ \(d_2\), chứa điểm O.
Bước 3: Vẽ đường thẳng \(d_3: x=5\) đi qua (5;0) và (5;1).
Lấy điểm O(0;0) không thuộc \(d_3\). Vì 0<5 nên O thuộc miền nghiệm
Miền nghiệm của BPT \(x \le 5\) là nửa mp bờ \(d_3\), chứa điểm O.
Bước 4: Vẽ đường thẳng \(d_4: x + y = – 1\) đi qua (-1;0) và (0;-1).
Lấy điểm O(0;0) không thuộc \(d_4\). Vì 0+0=0>-1 nên O thuộc miền nghiệm.
Miền nghiệm của BPT \(x + y \ge – 1\) là nửa mp bờ \(d_4\), chứa điểm O.
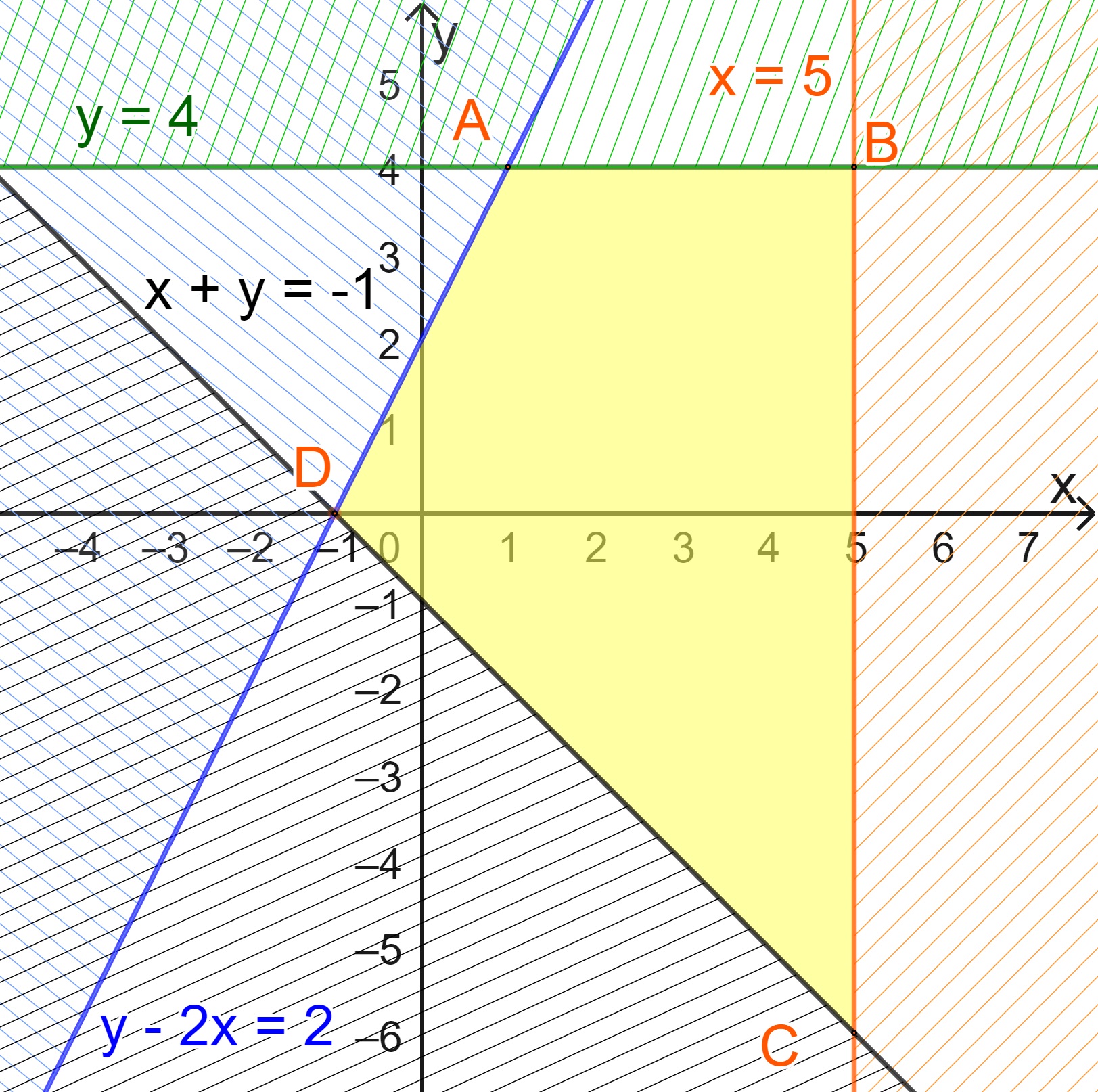
Miền biểu diễn nghiệm của hệ bất phương trình là miền tứ giác ABCD với
A(1;4); B(5;4), C(5;-6); D(-1;0).
Giá trị F tại các điểm A, B, C, D lần lượt là:
\(F\left( {1;4} \right) = – 1 – 4 = – 5\)
\(F\left( {5;4} \right) = – 5 – 4 = – 9\)
\(F\left( {5;-6} \right) = – 5 – (-6) = 1\)
\(F\left( { – 1;0} \right) = – \left( { – 1} \right) – 0 = 1\)
Vậy giá trị lớn nhất của biểu thức F(x;y) là 1 và giá trị nhỏ nhất của biểu thức F(x;y) là -9.
